研究背景

---

Nim游戏

1901年, Charles L. Bouton¹提出了Nim游戏的完整理论, Nim游戏是一种公平组合游戏, 游戏者轮流从几排棋子(或者任何道具)中选择一排, 再由这一排中取走一个或者多个. 在normal规则下, 最先不能进行操作的一方输.他在文章中给出了必胜策略及其证明, 即先手玩家有必胜的策略当且仅当各排棋子数的Nim和(即异或)不为零, 否则后手玩家有必胜的策略.

Sprague-Grundy定理

Sprague²与Grundy³在上世纪30年代各自独立发现了Sprague-Grundy定理, 表明任一normal规则下的公平组合游戏都等价于一个特定大小的Nim堆. 并且, normal规则下的公平组合游戏中的每个状态可以按如下函数赋予一个非负整数, 称为Sprague-Grundy函数^4-6: $$ \mathcal{G}(u) = \begin{cases} 0,&O(u) = \varnothing \\ Mex({\mathcal{G}({O(u)})}),&\text{其他} \end{cases} $$ 其中$Mex(S)$表示集合S外的最小非负整数, $O(u)$表示状态u下的所有合法操作, $G(O(u))$表示$O(u)$中所有元素的Sprague-Grundy函数值组成的集合.

正常$k$-染色游戏

2013年, Beaulieu, Burke和Duchêne⁷提出了一类特殊的组合游戏: 公平染色游戏. 该游戏具体描述为, 给定一个图, 两名游戏参与者根据染色规则轮流染图中的一个未被染色的顶点, 直到没有顶点可以被染为止.下面给出正常$k$-染色游戏的定义.

给定一个有限简单图$G$和$k$种颜色, 两名游戏参与者$P_{1}$和$P_{2}$轮流 选用一种颜色去染$G$中的一个未被染色的顶点, 相邻的两点不能染相同的颜 色, 先不能进行染色的玩家输. 该游戏被称为正常$k$-染色游戏.

游戏的位置

在一定的取胜规则下, 给定一个公平组合游戏的位置:

• 如果游戏者从这个位置开始没有策略赢得游戏, 则称该位置是 P-位置;
• 如果游戏者从这个位置开始存在策略赢得游戏, 则称该位置为 N-位置.

对于任意一个公平组合游戏, 在给定规则下, 所有 N-位置组成的集合与所有 P-位置组成的集合分割了所有的游戏位置^8-9, 即一个游戏位置要么是 N-位置, 要么是 P-位置.

游戏者符合游戏规则的操作被称为合法移动:

• 对于任一 N-位置, 存在一次合法移动可以将其变成 P-位置.
• 对于任一 P-位置, 任何一次合法移动都只能将其变成 N-位置.

研究内容

---

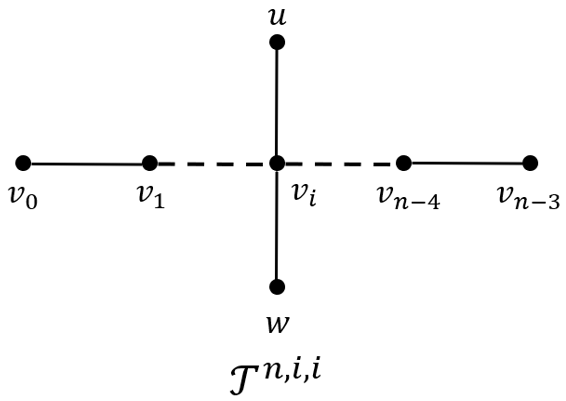
令$\mathcal{P}^{n}$为有$n$个顶点的路, 令$\mathcal{T}^{n,i,i}$为在$\mathcal{P}^{n-2}$的第$(i+1)$个顶点添加两个悬挂点$u$和$w$所得到的树, 其中$n \geq 5$且$1 \leq i \leq n-4$. 本文运用Sprague-Grundy函数理论，研究在$\mathcal{T}^{n,i,i}$上进行的正常2-染色游戏, 给出该游戏各位置的Grundy-值和最优策略.

研究方法

---

游戏的组合³

令$P$和$Q$是任意两个有限且互不影响的公平组合游戏, 则$\mathcal{G}(P+Q) = \mathcal{G}(P) \oplus \mathcal{G}(Q)$.

部分染色图的拆分

给定一部分染色图$G$,

• $\mathcal{G}(G) = Mex(\mathcal{G}(O(G))), $其中$O(G) =\{G_{v,B},G_{v,R} : v \in C(G)\}$;
• 对任意的$v \in C(G)$, 若$v$是$G$的割点且$V_{1},V_{2},\ldots,V_{k}$分别是$G-\{v\}$的各个连通分量的顶点集, 则$$\mathcal{G}(G_{v,B}) = G_{v,B}^{1} \oplus G_{v,B}^{2} \oplus \ldots \oplus G_{v,B}^{k},$$

其中$G_{v,B}^{1}, G_{v,B}^{2},\ldots, G_{v,B}^{k}$分别是由$V_{1}\cup\{v\},V_{2}\cup\{v\},\ldots, V_{k}\cup\{v\}$诱导的$G$的子图. 对于$\mathcal{G}(G_{v,R})$同理.

已有结论

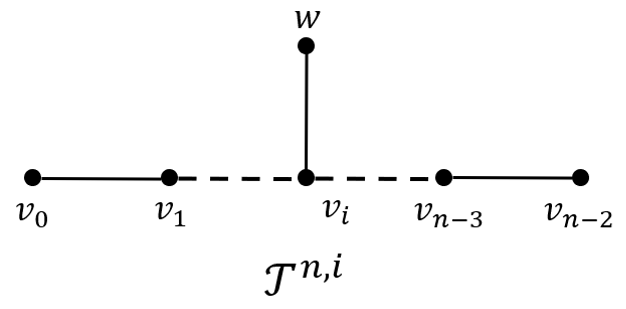
Zhao¹⁰给出了仅有一个悬挂点的$\mathcal{T}^{n,i}$上正常2-染色游戏的Grundy函数值与最优策略.

一些繁琐的定义

---

为了更好地阐述结论, 需要使用如下记号:

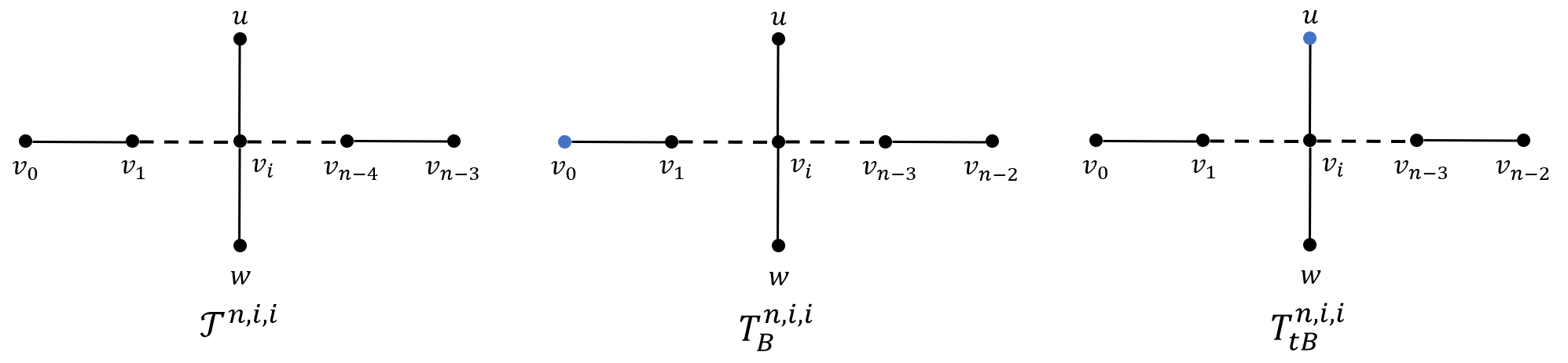
1. 用$\mathcal{T}^{n,i,i}$表示将顶点依次为$v_{0},v_{1},\ldots v_{n - 3}$的路$\mathcal{P}^{n - 2}$上添加两个新的顶点$u,w$, 同时添加$u$与$v_{i}$相关联的边、$w$与$v_{i}$相关联的边所得到的树;
2. 用$T_{B}^{n,i,i}$表示将$\mathcal{T}^{n + 1,i,i}$中的顶点$v_{0}$进行染色所得到的部分染色树;
3. 用$T_{tB}^{n,i,i}$表示将$\mathcal{T}^{n + 1,i,i}$中的顶点$u$进行染色所得到的部分染色树;

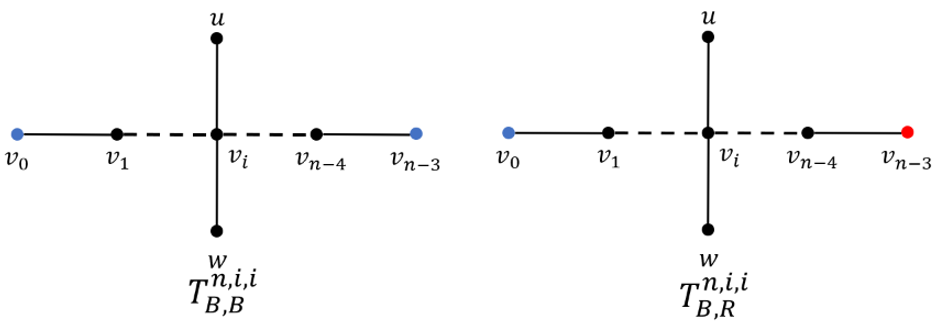
4. 用$T_{B,B}^{n,i,i}$表示将$\mathcal{T}^{n + 2,i,i}$中的顶点$v_{0},v_{n-1}$染相同颜色所得到的部分染色树;
5. 用$T_{B,R}^{n,i,i}$表示将$\mathcal{T}^{n + 2,i,i}$中的顶点$v_{0},v_{n-1}$染不同颜色所得到的部分染色树;
6. 用$T_{B,tB}^{n,i,i}$表示将$\mathcal{T}^{n + 2,i,i}$中的顶点$v_{0},u$染相同颜色所得到的部分染色树;
7. 用$T_{B,tR}^{n,i,i}$表示将$\mathcal{T}^{n + 2,i,i}$中的顶点$v_{0},u$染不同颜色所得到的部分染色树;

8. 用$T_{B,B,tR}^{n,i,i}$表示将$\mathcal{T}^{n+3,i,i}$中的顶点$v_{0}$和$v_{n}$染相同颜色, 将$u$染为另一颜色所得到的部分染色树;
9. 用$T_{B,R,tR}^{n,i,i}$表示将$\mathcal{T}^{n+3,i,i}$中的顶点$v_{0}$染一种颜色, 将$u$和$v_{n}$染为另一颜色所得到的部分染色树;
10. 用$T_{B,B,tB}^{n,i,i}$表示将$\mathcal{T}^{n+3,i,i}$中的顶点$v_{0},v_{n}$和$u$染相同颜色所得到的部分染色树;
11. 用$T_{B,R,tB}^{n,i,i}$表示将$\mathcal{T}^{n+3,i,i}$中的顶点$v_{0}$和$u$染相同颜色, 将$v_{n}$染为另一颜色所得到的部分染色树.

结论

---

三个端点被染色的$\mathcal{T}^{n,i,i}$的Grundy函数值

设 $n \geq 2,1 \leq i \leq \frac{n}{2}$, 则： $$ \mathcal{G}(T_{B, B, tR}^{n, i, i})=\begin{cases} (n-2) \oplus 1,&i=1 \\ 3,&n=6 \text { and } i=3 \\ 2,&n \neq 2, n \neq 6 \text { and } i=\frac{n}{2} \\ 0,&\text {else} \end{cases}\\ \mathcal{G}(T_{B, R, tR}^{n, i, i})=\begin{cases} (n-2) \oplus 1,&i=1 \\ 2,&n=7 \text { and } i=3 \\ 3,&n \neq 3, n \neq 7, n \equiv 3 \bmod 4 \text { and } i=\frac{n-1}{2}\\ 1,&\text {else} \end{cases}\\ \mathcal{G}(T_{B, B, tB}^{n, i, i})=\begin{cases} n-3,&i=2, n \equiv 1 \bmod 2 \text { or } n \equiv 2 \bmod 4 \\ n-1,&i=2, n \equiv 0 \bmod 4 \\ 3,&n=8 \text { and } i=4 \\ 2,&n \neq 8 \text { and } i=\frac{n}{2} \\ 0,&\text {else} \end{cases}\\ \mathcal{G}(T_{B, R, tB}^{n, i, i})=\begin{cases} n-3,&i=2, n \equiv 1 \bmod 2 \text { or } n \equiv 0 \bmod 4 \\ n-1,&i=2, n \equiv 2 \bmod 4 \\ 3,&n \equiv 3 \bmod 4 \text { and } i=\frac{n-1}{2} \\ 1,&\text {else} \end{cases} $$

两个端点被染色的$\mathcal{T}^{n,i,i}$的Grundy函数值

设$n \geq 3$,$1 \leq i \leq \frac{n-1}{2}$, 则 $$ \mathcal{G}(T_{B,B}^{n,i,i}) = \begin{cases} 3,&n = 3 \\ 1,&\text{其他} \end{cases}\\ \mathcal{G}(T_{B,R}^{n,i,i}) = \begin{cases} 2,&n = 4 \\ 0,&\text{其他} \end{cases} $$

设$n \geq 3$,$1 \leq i \leq n-2$, 则 $$ \mathcal{G}(T_{B,tB}^{n,i,i}) = \begin{cases} n,&i=1,n\text{为奇数}\\ n-3,&i=1,n\text{为偶数}\\ 0,&i=2,n\text{为奇数}\\ 1,&i=1,n\text{为偶数}\\ 7,&i=5,n=10\\ 8,&i=5,n=11\\ 7,&i=7,n=12\\ 8,&i=7,n=13\\ n-i+1,&i=2^{m}-1, n=3 \times 2^{m-1}, m \geq 2, (i \neq 7 \text{或} n \neq 12)\\ n-i+1,&i=2^{m}-1, n \geq 3 \times 2^{m-1}+1, n \equiv 2^{m-1}+1 \bmod 2^{m}, m \geq 2, (i \neq 7 \text{或} n \neq 13)\\ n-i-1,&i \geq 3, i \text{为奇数}, i+2 \leq n \leq 2i-1, (i \neq 7 \text{或} n \neq 12), (i \neq 7 \text{或} n \neq 13)\\ n-i-1,&i \geq 3, i \text{为奇数}, n=2i+2\\ n-i-1,&i \geq 3, i \text{为奇数}, n \geq 2i+3, n \text{为奇数}\\ n-i+1,&i \geq 3, i \text{为奇数}, (n=2i \text{或} n=2i+1), i \neq 3, i \neq 5\\ n-2i-1,&i \geq 3, i \text{为奇数}, n \geq 2i+4, n \text{为偶数}\\ n-i-3,&i=4, n \geq 8, n \text{为偶数}\\ n-i-1,&i \geq 4, i \text{为偶数}, i+2 \leq n \leq 2i-1\\ n-i-1,&i \geq 6, i \text{为偶数}, n \geq 2i, n \text{为偶数}\\ n-2i-1,&i \geq 4, i \text{为偶数}, n \geq 2i+1, \text{为奇数} \end{cases}\\ \mathcal{G}(T_{B,tR}^{n,i,i}) = \begin{cases} 0,&i=1,n\text{为奇数}\\ 1,&i=1,n\text{为偶数}\\ n-5,&i=2,n\text{为奇数}\\ n-2,&i=1,n\text{为偶数}\\ n-2i-1,&i=3, n \geq 7, n \text{为奇数}\\ 6,&i=6,n=11\\ 9,&i=6,n=12\\ 6,&i=4,(n=7 \text{或} n=8)\\ 6,&i=8,n=13\\ n-i+2,&i=2^{m}, n=3 \times 2^{m-1}+1, m \geq 4\\ (n-i-1) \oplus 1,&i \geq 3, i \text{为奇数}, i+2 \leq n \leq 2i+1, (i \neq 3 \text{或} n \neq 7)\\ n-2i-1,&i \geq 3, i \text{为奇数}, n \geq 2i+2, n \text{为偶数}\\ n-i-2,&i \geq 3, i \text{为奇数}, n \geq 2i+3, n \text{为奇数}\\ (n-i-1) \oplus 1,&i \geq 4, i \text{为偶数}, i+2 \leq n \leq 2i-2, (i \neq 8 \text{或} n \neq 13)\\ n-i,&i \geq 4, i \text{为偶数}, (n=2i \text{或} n=2i+1), (i \neq 4 \text{或} n \neq 8), (i \neq 6 \text{或} n \neq 12)\\ n-i+2,&i \geq 4, i \text{为偶数}, n=2i-1, (i \neq 4 \text{或} n \neq 7), (i \neq 6 \text{或} n \neq 11)\\ n-i-2,&i \geq 4, i \text{为偶数}, n \geq 2i+2, n \text{为偶数}\\ n-2i-1,&i \geq 4, i \text{为偶数}, n \geq 2i+3, n \text{为奇数} \end{cases} $$

一个端点被染色的$\mathcal{T}^{n,i,i}$的Grundy函数值

设$n \geq 4$,$1 \leq i \leq n-3$, 则 $$ \mathcal{G}(T_{B}^{n,i,i}) = \begin{cases} n-2,&i=1, n \text{为偶数}\\ n-5,&i=1, n \text{为奇数}\\ 7,&n=8, i=4\\ 6,&n=9, i=5\\ n-2,&\text{其他} \end{cases} $$

设$n \geq 4$,$1 \leq i \leq \frac{n-2}{2}$, 则 $$ \mathcal{G}(T_{tB}^{n,i,i}) \begin{cases} \neq 0,& n \text{为偶数}\\ \neq 0,& n \geq 3i+4, (n \neq 2i+9 \text{或} n \neq i+13), (n \neq 2i+9 \text{或} n \neq i+14)\\ \neq 0,& i=2^{m-1}, n=4i+3, m \geq 2\\ \neq 0,& i=2^{m-1}, n=4i+5, m \geq 4\\ \neq 0,& n=2i+2^{m}+3, i \geq 2^{m-1}+1, i \equiv 2^{m-1}+1 \bmod 2^{m}, m \geq 2\\ \neq 0,& i \text{为偶数}, n=2i+3\\ \neq 0,& i \text{为偶数}, i \geq 4, n=3i+1/3i+3\\ \neq 0,& i \text{为偶数}, i \geq 6, n=3i+5\\ \neq 0,& i \text{为偶数}, n \geq 3i+6\\ \neq 0,& i \text{为奇数}, i \geq 5, n=2i+3\\ \neq 0,& i \text{为奇数}, n=2i+5\\ \neq 0,& i \text{为奇数}, 2i+5 \leq n \leq 3i\\ \neq 0,& i \text{为奇数}, n \geq 3i+4\\ =0,& \text{其他} \end{cases} $$

$\mathcal{T}^{n,i,i}$上的正常2-着色游戏

设$n \geq 5$,$1 \leq i \leq \frac{n-3}{2}$, 则 $$ \mathcal{G}(\mathcal{T}^{n,i,i}) \begin{cases} \neq 0,& i\text{为奇数}, n=2i+4/2i+5\\ \neq 0,& i=2, n=16\\ \neq 0,& n \geq 2i+7, n \text{为偶数}, (n \neq 15 \text{或} n \neq 2i+11), (n \neq 17 \text{或} n \neq 2i+13)\\ \neq 0,& n=2i+3\\ \neq 0,& \mathcal{G}(T_{tB}^{n-1,i,i})=0\\ =0,& \text{其他} \end{cases} $$ 其中 $$ \mathcal{G}(T_{tB}^{n-1,i,i}) \begin{cases} \neq 0,& n \text{为奇数}\\ \neq 0,& n \geq 3i+5, (n \neq 2i+10 \text{或} n \neq i+14), (n \neq 2i+10 \text{或} n \neq i+15)\\ \neq 0,& i=2^{m-1}, n=4i+4, m \geq 2\\ \neq 0,& i=2^{m-1}, n=4i+6, m \geq 4\\ \neq 0,& n=2i+2^{m}+4, i \geq 2^{m-1}+1, i \equiv 2^{m-1}+1 \bmod 2^{m}, m \geq 2\\ \neq 0,& i \text{为偶数}, n=2i+4\\ \neq 0,& i \text{为偶数}, i \geq 4, n=3i+2/3i+4\\ \neq 0,& i \text{为偶数}, i \geq 6, n=3i+6\\ \neq 0,& i \text{为偶数}, n \geq 3i+7\\ \neq 0,& i \text{为奇数}, i \geq 5, n=2i+4\\ \neq 0,& i \text{为奇数}, n=2i+6\\ \neq 0,& i \text{为奇数}, 2i+6 \leq n \leq 3i+1\\ \neq 0,& i \text{为奇数}, n \geq 3i+5\\ =0,& \text{其他} \end{cases} $$

参考文献

---

[1] BOUTON C L. Nim, a game with a complete mathematical theory[J]. Annals of Mathematics, 1901, 3(1/4): 35-39.

[2] SPRAGUE R. Über mathematische kampfspiele[J]. Tohoku Mathematical Journal, First Series, 1935, 41: 438-444.

[3] GRUNDY P M. Mathematics and games[J]. Eureka, 1939, 2: 6-9.

[4] LANDMAN H. A simple FSM-based proof of the additive periodicity of the Sprague-Grundy function of Wythoff’s game[C]//More Games of No Chance, Proc. MSRI Workshop on Combinatorial Games: volume 42. 2000: 383-386.

[5] JIAO Y. On the Sprague-Grundy values of the $\mathcal{F}$-Wythoff Game[J]. The Electronic Journal of Combinatorics, 2013: P14-P14.

[6] LARSSON U, RUBINSTEIN-SALZEDO S. Grundy values of Fibonacci nim[J]. International Journal of Game Theory, 2016, 45(3): 617-625.

[7] BEAULIEU G, BURKE K, DUCHÊNE É. Impartial coloring games[J]. Theoretical Computer Science, 2013, 485: 49-60.

[8] FRAENKEL A S. Complexity, appeal and challenges of combinatorial games[J]. Theoretical Computer Science, 2004, 313(3): 393-415.

[9] GARDNER M. Mathematical games[J]. Scientific American, 1970, 222(6): 132-140.

[10] ZHAO X, CHEN S. Proper 2-coloring game on some trees[J]. Theoretical Computer Science, 2019, 778: 1-18.